The aim of this lecture is to introduce the basic mathematical concepts behind PHOENICS. An overview of the solution algorithms used is given in a separate lecture.
Topics Covered
Variables
Equations
Boundary conditions
Classification
Variables may be thought of as being:
In each case, they can be further subdivided into scalar and vector quantities:
The quantities defining the problem geometry can also be divided into scalar and vector categories:
The distinction between scalar and vector is important, because each is stored at a different location in space:
Nomenclature - A compass-point notation is used, as shown below
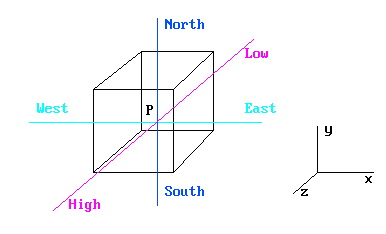
P = Cell center
N,S,E,W,H,L = Neighbour-cell centers
S -> N = Positive IY
W -> E = Positive IX
L -> H = Positive IZ
T = Cell center at previous time step
An array of cells with the same IZ is referred to as a SLAB.
Steady or Transient
Steady-State Problems - PHOENICS can proceed directly to the steady-state solution. It is not necessary to march through time to reach the steady state.
Transient Problems - PHOENICS can cope with constant and variable time steps. The time step size can be a function of time.
Storage locations
Vector quantities are computed by reference to cells which are staggered with respect to the scalar cells.
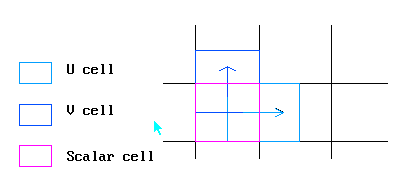
3 velocities and 1 scalar share the same cell index (IX,IY,IZ).
Any scalar or vector quantity can only be referenced by a unique (IX,IY,IZ) index. Thus the velocity on the West face of the cell P above 'belongs' to the West scalar cell.
Types of Grid
PHOENICS grids are structured - cells are topologically Cartesian brick elements.
PHOENICS grids may be :
In all cases, the grid distribution can be non-uniform in all coordinate directions.
For cylindrical-polar coordinates, the following orientation is used:
Basic form
The basic balance, or conservation equation is just:
Outflow from cell - Inflow into cell = net source within cell
The quantities being balanced are the dependent variables from the earlier panel:
Terms
The terms appearing in the balance equation are:
The single phase conservation equation solved by PHOENICS can be written as:
![]()
where: φ - the variable in question
ρ - density
![]() -
vector velocity
-
vector velocity
![]() - the
diffusive exchange coefficient for f
- the
diffusive exchange coefficient for f
![]() - the
source term
- the
source term
Particular Forms
Particular examples are:
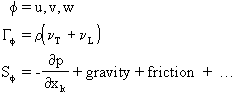 Momentum
Momentum
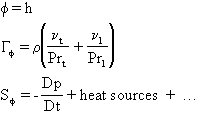 Enthalpy
Enthalpy
 Continuity
Continuity
where ![]() are the turbulent and laminar viscosities, and Prt, Prl are the
turbulent and laminar Prandtl/Schmidt Numbers.
are the turbulent and laminar viscosities, and Prt, Prl are the
turbulent and laminar Prandtl/Schmidt Numbers.
Numerical solution
The balance equations cannot be solved numerically in differential form. Hence, PHOENICS solves a finite-volume formulation of the balance equation.
The FVE's are obtained by integrating the differential equation over the cell volume.
Interpolation assumptions are required to obtain scalar values at cell faces and vector quantities at cell centers.
No Taylor series expansion or variational principle is used.
Finite Volume Form
After integration, the FVE has the form:
![]()
where:
![]() (by
continuity)
(by
continuity)
The neighbour links, the a's, have the form
![]()
convection diffusion transient
Correction Form
The equation is cast into correction form before solution.
In correction form, the sources are replaced by the errors in the real equation, and the coefficients may be only approximate. The corrections tend to zero as convergence is approached, reducing the possibility of round-off errors affecting the solution.
The neighbor links:
Transient phenomena are always parabolic - the future cannot affect the past.
This allows for a marching solution, with only the current and previous time step values required. Reducing time step size thus does not increase memory requirements.
Steady-state flows can also be parabolic if the flow is unidirectional, and diffusion in that direction is negligible.
Solution can now be achieved by marching through space, with considerable saving in memory requirement. In PHOENICS, such marching is always in the Z (or K) direction.
A fuller account of parabolic flows is provided here.To close the equation set, auxiliary equations must be provided for:
There may also be 'artificial' auxiliary equations, such as
All of the above may be functions of some or all of the other solved-for variables, or auxiliary quantities, resulting in a highly non-linear set of equations.
Introduction
Another lecture in this series is devoted to Boundary Conditions in PHOENICS, so only a brief overview and introduction will be presented here.
Boundary Conditions can be:
General form
Boundary Conditions are represented in PHOENICS as linearized sources for cells adjacent to boundaries:
![]()
aBC is termed the COEFFICIENT.
![]() is
termed the VALUE.
is
termed the VALUE.
aBC is added to aP , and ![]() is added to
the RHS of the equation for
is added to
the RHS of the equation for ![]() .
.
![]()
Particular forms
For a fixed value boundary, aBC is made very big. The effect is:
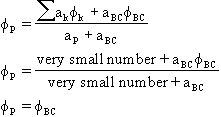
For a fixed flux boundary, aBC is made very small, and ![]() is set to the
required flux.
is set to the
required flux.
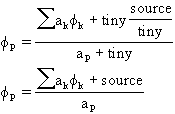
Linear and non-linear conditions can be set by appropriate prescription of aBC
and ![]()