Encyclopaedia Index
2.4 In-Form objects
Contents
- Definition
- Cell-enclosing (i.e. volumetric) shapes; box, sphere, ellipsoid
- Cell-cutting (i.e. sub-grid) shapes; point, line, plane
- Shapes made by restricting the PATCH size
- Shapes made by using non-constant parameters
- Shapes made by adding and subtracting
- 'Negative' objects
- Positions varying with time
- Shapes varying with time
(a) Definition
Two kinds of object
- VR objects
- Since the introduction in 1995 of the 'Virtual-Reality'
user interface, PHOENICS has made extensive use of 'objects'.
[Click
here
for the relevant Encyclopaedia entry].
- Their shapes have been
described by way of files, with .dat extensions, which define the
locations of the vertices of the facets of which their surfaces are
composed.
- Their positions, together with problem-specific re-sizings and
re-orientations,
have been conveyed to the PHOENICS solver-module EARTH by way of the
file named FACETDAT.
- They will be referred to as Virtual-Reality objects below.
- In-Form objects
- Similarities and differences between the two kinds of
object are:
- Like Virtual-Reality objects, In-Form objects can be used for
defining the locations of cells in into which initial values and
sources are to be introduced.
- Both kinds of objects may change their positions with time; but
only In-Form objects can also change their shape.
- However, whereas VR-objects are easily brought into a simulation
scenario, and then located and resized by means
of the menus and dialog boxes of the VR-Editor, this is not yet
(March 2009) possible for In-Form objects.
- If any cell is occupied by two or more VR objects,
only those
initial values and sources which pertain to the object which appears
last in the Q1 file are transmitted to that cell.
For In-Form objects, this is true in respect of initial values also;
but the sources are added together.
In this respect they are similar to PIL PATCHes and dissimilar from
VR objects.
- Moreover, because the information about In-Form objects is processed
in EARTH later than that concerning VR objects, and without
checking what has gone before, In-Form objects can be said to
prevail over VR objects whenever both claim ownership of the same
cell.
Of course, since all In-Form formulae can be supplied with 'with
(if(...))' conditions, checking can be enforced, if desired.
- Another point of difference is that whereas VR objects can be used
for setting material properties only by way of initial values,
In-Form objects allow such properties to be set via formulae which
call for changes in response to varying pressure, temperature
and other variables.
- Lastly, VR objects can be used for activating the
PARSOL treatment of
the 'cut cells' which its presence creates.
With one exception (viz.the
plane-quadrilateral), In-Form objects can not be so used at the
present time.
They can be used however for computing the volume and
area porosities of the cells which they affect.
- Work is in progress which should enable all appropriate In-Form
objects to activate PARSOL by the end of 2011.
How In-Form objects are defined
In-Form objects are created and defined by means of
statements of the following format:
(INFOB at PATCHNAME is FORMULA with infob_OBJNAME!options)
Here:
- 'INFOB' is a keyword, like 'PROPERTY', 'STORED' and 'SOURCE',
which indicates what kind of information is to follow.
- 'PATCHNAME' is the user-chosen name in a PIL PATCH
statement, which defines the 4-dimensional block of space-time within which the object is
(or parts of it are) somewhere to be found;
The PATCH statement must be placed higher in the Q1 file than the INFOB
statement referring to it.
- 'FORMULA' is a character string which defines the shape and
position of the object in space and time. It may contain functions,
like any other In-Form formula; but some functions (BOX, SPHERE, and others described below) are significant for In-Form objects alone.
- 'OBJNAME' is the user-chosen name (of which only the first 8
characters are significant) of the object.
- 'options' refers to any other of the conditions listed in
Appendix 3 of the In-Form documentation; but one option, viz.
PORO, has significance for In-Form objects only.
Two kinds of PATCH
Until April 2009, the space-time location of PIL PATCHes was almost invariably defined by way of the indices IXF, IXL, IYF, IYL, IZF, IZL, ITF, and ITL.
Partly because this conflicted in style with the grid-independent setting of In-Form objects, a new kind of patch, the so-called
'dot-patch' has now been introduced.
This sets the location by way of real-number arguments: RXF, RXL, RYF, RYL, RZF, RZL, RTF, and RTL. These represent the geometric coordinates, normalised by reference to XULAST, YVLAST, ZWLAST and TLAST, of the eight faces of the space-time block within the In-Form object is to be found.
Such patches, which are marked by having a dot, ., as the first character of their names retain their positions when the grid is changed.
It is for this reason that the use of dot-patches is to be preferred ot those of the old indicial type.
How In-Form objects are used
In-Form objects can be used for setting initial values, properties and
sources by means of statements such as:
(INITIAL of PRPS at PATCHNAME is 67. with infob_OBJNAME)
(PROPERTY of RHO1 at PATCHNAME is 1.e-5*(P1+:PRESS0:) with infob_OBJNAME)
(SOURCE of TEM1 at PATCHNAME is xg+yg with infob_OBJNAME)
Thus the specific name of the object appears as an 'option' i.e. a 'modifier' of the source statement, Without it, the source would appear in all the cells of the patch.
It is however not necessarily the only one.
For example, the above line could be modified to:
(SOURCE of TEM1 at PATCHNAME is xg+yg with infob_OBJNAME!fixval)
or(SOURCE of TEM1 at PATCHNAME is xg+yg with infob_OBJNAME!fixflu)
If no additional option is added, the default !fixflu is presumed.
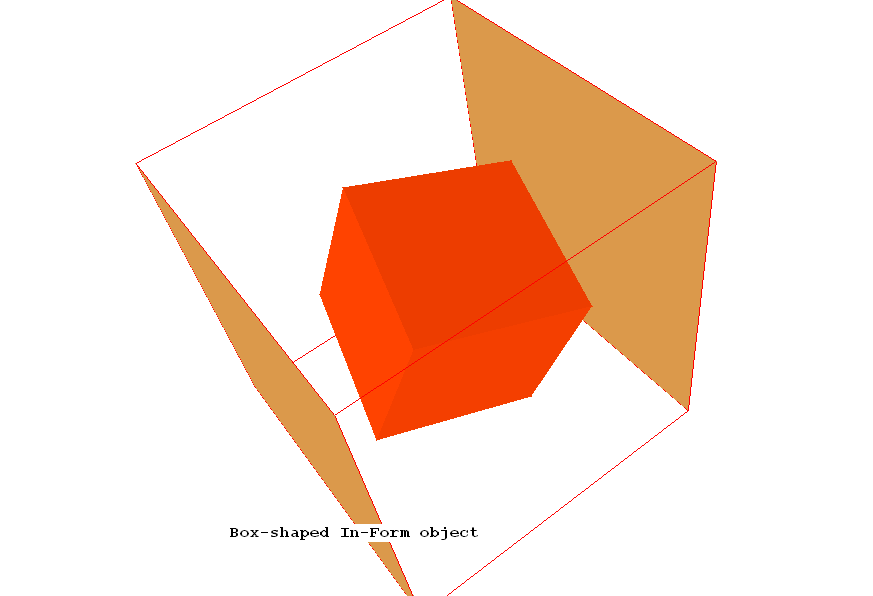
Currently available object shapes
At the present time (April 2009), six basic shapes of In-Form objects,
and of two kinds, are provided, namely:
- Cell-enclosing (also called 'volumetric') shapes, namely:
- BOX,
- SPHERE, and
- ELLIPSOID,
and
- cell-penetrating (also called 'sub-grid') shapes, namely:
- POINT,
- LINE, and
- PLANE QUADRILATERAL.
However, objects of much more complex shapes may be constructed by using
one or more of the following techniques:
- restricting the dimensions of the PATCH so that parts of the
specified shape lie outside it;
- setting the arguments of the basic-shape functions (to
be described) as expressions rather than constants; and
- by 'adding' and 'subtracting' several basic shapes.
Further, the 'subtraction' feature permits creation of 'negative'
objects, i.e. those in which the object attributes are applied to
those cells which the object does not enclose or penetrate rather than to those
which it does.
(b) The basic cell-enclosing (i.e. volumetric)
shapes
Each of the basic shapes of the first group is described by an In-Form
function possessing (nearly) the same name as the shape (but ELLIPSOID is
shortened to ELLPSD). They will now be described, in turn.
The BOX function
The format governing the use of BOX in INFOB statements is indicated by
the following example:
(INFOB at BOXPAT1 is BOX(arguments) with INFOB_BOX1)
where BOXPAT1 and BOX1 are names chosen freely by the user.
The arguments in question are as follows:
BOX(x0,y0,z0,xsize,ysize,zsize,alpha,beta,theta)
where
x0 = X-coordinate of west south low corner of box, in meters
y0 = Y-coordinate of west south low corner of box, in meters
z0 = Z-coordinate of west south low corner of box, in meters
xsize = X-size of box side, in meters
ysize = Y-size of box side, in meters
zsize = Z-size of box side, in meters
alpha = angle rotating around x axis, in radians
beta = angle rotating around y axis, in radians
theta = angle rotating around z axis, in radians
The six position and size arguments correspond to those which are used for VR-objects; but the three rotation arguments follow a different convention.
Library case 383
illustrates the use of the box function for the
creation of a box in a cubical domain, with all its rotations equal to
0.25 radians, by means of the following statements:
inform11begin
(stored of mark at patch1 is 1.0 with infob_1) ! MARK object
(initial of prps is 100 with infob_1) ! initialise PRPS
real(x0,y0,z0,xs,ys,zs,al,be,th) ! declarations
x0=xulast/4 ! x/y/z position of box
y0=yvlast/4 !
z0=zwlast/4 !
xs=xulast/2 ! x/y/z size of box
ys=yvlast/2 !
zs=zwlast/2 !
al=0.25 ! alpha/beta/theta angles of coordinate system
be=0.25 ! of box
th=0.25 !
(infob at patch1 is box(x0,y0,z0,xs,ys,zs,al,be,th) with infob_1)
inform11end
Here, in order to make its shape and position
visible in PHOTON and the VR
VIEWER, the variable MARK has been stored and given the value of 1.0 for
all the cells enclosed by the object.
It will be noticed that the often-convenient device is adopted of defining
x0, y0, etc as real variables, and setting their values in statements
which
precede (INFOB ... .
In this case, the values are constants, which would not be difficult to
read if
inserted directly as:
BOX(:xulast/4:,:yvlast/4:, etc) ;
but, were
they long formulae, their
appearance following BOX( would make the line tiresomely long.
A PHOTON plot of the case-383 BOX object is shown
here. It was
created by the sur mark x 0.99 and sur mark y 0.99
commands.
In this example, each parameter is a constant; but each could have been
a function, as will be illustrated in section (e) below.
The SPHERE function
The format governing the use of SPHERE in INFOB statements is similar to
that of BOX, namely:
(INFOB at SPHPAT1 is SPHERE(arguments) with INFOB_SPH1)
where SPHPAT1 and SPH1 are names arbitrarily chosen by the user.
It has only four arguments however, namely:
SPHERE(xc, yc, zc, radius)
where
xc = x coordinate of the centre, in meters
yc = y coordinate of the centre, in meters
zc = z coordinate of the centre, in meters
radius = radius of the sphere, in meters
because rotations about its centre cannot change its shape.
When the calculation is being carried out with a Cartesian grid, the
coordinate system of the sphere coincides with the
coordinate system of the calculation domain.
However, when the calculation is being carried out with a
cylindrical-polar-coordinate grid,
the cartesian coordinate system of the sphere has its origin at the bottom
left-hand corner of a rectangular box which circumscribes a cylinder of radius
RINNER+YVLAST.
In this case, cartesian coordinates xc and yc are related to the polar
coordinates xp and yp by the relations:
xc=(yvlast+rinner) + (yp + rinner) * sin(xp)
and
yc=(yvlast+rinner) + (yp + rinner) * cos(xp)
The Z coordinates of the origins and the directions of Z axes of both coordinate
systems coincide with one another.
Library case
772
creates an In-Form object,
namely a sphere with its centre on the axis of a polar grid, by means
of:
(INFOB at PATCH1 is SPHERE(10, 10, 10, 5) with INFOB_1)
The PHOTON plot displayed
here
reveals the result.
In this case, it may be noted, xce, yce and zce are declared as
character variables. This is the preferable procedure when the
possible use of formulae as arguments is to be provided for.
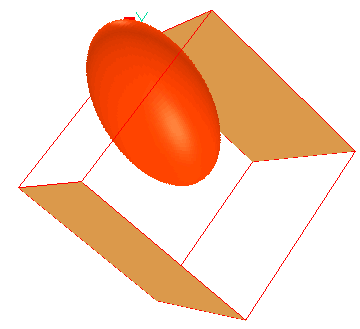
The ELIPSOID function
The format governing the use of ELLIPSOID in INFOB statements is indicated by
the following example:
(INFOB at ELLPAT1 is ELLPSD(arguments) with INFOB_ELL1)
where ELLPAT1 and ELL1 are names chosen freely by the user.
The arguments in question are as follows:
ELLPSD(x0,y0,z0,xrad,yrad,zrad,alpha,beta,theta)
where
x0 = X-coordinate of the centre of the ellipsoid, in meters
y0 = Y-coordinate of the centre of the ellipsoid, in meters
z0 = Z-coordinate of the centre of the ellipsoid, in meters
xrad = X-direction radius, in meters
yrad = Y-direction radius, in meters
zrad = Z-direction radius, in meters
alpha = angle rotating around x axis, in radians
beta = angle rotating around y axis, in radians
theta = angle rotating around z axis, in radians
Library case 384
illustrates the use of the ELLPSD function for the
creation of an ellipsoid in a cubical domain, with all its rotations equal to
0.25 radians, by means of the
following statements:
inform11begin
(stored of mark at patch1 is 1.0 with infob_1) ! MARK object
(initial of prps is 100 with infob_1) ! initialise PRPS
real(x0,y0,z0,xs,ys,zs,al,be,th) ! declarations
x0=xulast/4 ! x/y/z position of ellipsoid
y0=yvlast/4 !
z0=zwlast/4 !
xs=xulast/2 ! x/y/z radius of ellipsoid
ys=yvlast/3 !
zs=zwlast/4 !
al=0.25 ! alpha/beta/theta angles of coordinate system
be=0.25 ! of ellipsoid
th=0.25 !
(infob at patch1 is ellpsd(x0,y0,z0,xs,ys,zs,al,be,th) with infob_1)
inform11end
An image representing the ellipsoid created by core-input-file-library case 384 can be seen by clicking
here.
Another example of the use of ellipsoid objects is core-library
case 162, wherein the ellipsoid is given such an extremely
large y-direction radius that, within the domain of study, it can be regarded
as a cylinder.
It is indeed used there to represent a cylindrical pipe with an aperture
in its walls from which gas is released into the atmosphere,
A fuller description of the situation can be found by
clicking here,
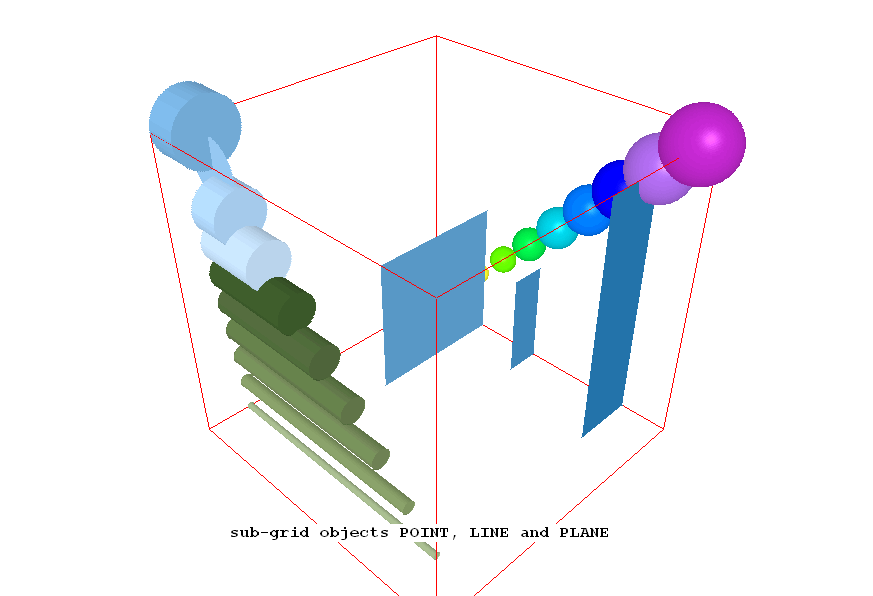
(c) The basic cell-cutting (i.e. sub-grid) shapes
Sub-grid objects are those of which one of the dimensions is smaller than
that of the computational grid.
The three basic shapes of this kind are: POINT, LINE and PLANE; and to each
there corresponds an In-Form function.
The POINT function
The format governing the use of POINT in INFOB statements is indicated by
the following example:
(INFOB at PNTPAT1 is POINT(arguments) with INFOB_PNT1!options
where PNTPAT1 and PNT1 are names chosen freely by the user.
The arguments in question are as follows:
POINT(x0,y0,z0,nomdiam)
where:
x0 = X-coordinate of the point, in meters,
y0 = Y-coordinate of the point, in meters,
z0 = Z-coordinate of the point, in meters,
nomdiam = nominal diameter of the point.
The setting of point objects is exemplified in Core Library case
385, as seen by
clicking here.
The LINE function
The format governing the use of Line in INFOB statements is indicated by
the following example:
(INFOB at LINPAT1 is POINT(arguments) with INFOB_LIN1!optionsV
where LINPAT1 and LIN1 are names chosen freely by the user.
The arguments in question are as follows:
LINE(x0,y0,z0,x1,y1,z1,nomdiam)
where:
x0 = X-coordinate of the start point, in meters,
y0 = Y-coordinate of the start point, in meters,
z0 = Z-coordinate of the start point, in meters,
x1 = X-coordinate of the end point, in meters,
y1 = Y-coordinate of the end point, in meters,
z1 = Z-coordinate of the end point, in meters,
nomdiam = nominal diameter of the line.
The setting of line objects is exemplified in Core Library case
385, as seen by
clicking here.
The PLANE function
The format governing the use of PLANE in INFOB statements is indicated by
the following example:
(INFOB at PLAPAT1 is PLANE(arguments) with INFOB_PLA1!options)
where PLAPAT1 and PLA1 are names chosen freely by the user.
The arguments in question are as follows:
PLANE(
where:
x0 = X-coordinate of 1st vertex, in meters,
y0 = Y-coordinate of 1st vertex, in meters,
z0 = Z-coordinate of 1st vertex, in meters,
x1 = X-coordinate of 2nd vertex, in meters,
y1 = Y-coordinate of 2nd vertex, in meters,
z1 = Z-coordinate of 2nd vertex , in meters,
x2 = X-coordinate of 3rd vertex , in meters,
y2 = Y-coordinate of 3rd vertex, in meters,
z2 = Z-coordinate of 3rd vertex, in meters,
x3 = X-coordinate of 4th vertex, in meters,
y3 = Y-coordinate of 4th vertex, in meters,
z3 = Z-coordinate of 4th vertex, in meters,
nomdiam = nominal thickness of the plane.
Not all shapes are permissible, as shown here.
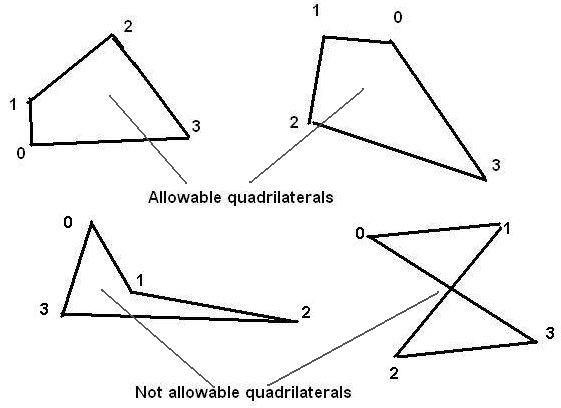
Further, if the user inadvertently selects four points which do not lie in a plane, the fact is detected by PHOENICS, which thereupon changes the 9th co-ordinate to such a value (there can be only one) which causes the fourth vertex to lie in the plane of the other three; or, if that is not possible, it does it for the 8th or the 7th.
It is sometimes useful to distinguish the two sides of the plane as being 'positive' or 'negative'. The convention adopted is that the positive side of the plane is that in which one must look if the first, second, third and fourth points are to apppear in clock-wise order.
Thus we are looking in the positive direction of the top-left quadrilateral above (and therefore seeing its negative side:
and we are looking in the negative direction at the top-right quadrilateral (and therefore seeing its positive side.
The setting of plane objects is exemplified in Core Library case
385,
which employs PIL do loops to enable many objects to be set, in orderly groups
Graphical display
All the objects introduced in case 385 are displayed here by way of
surface-value plots of PRPS which is specified as 100 within all the
intersected cells.
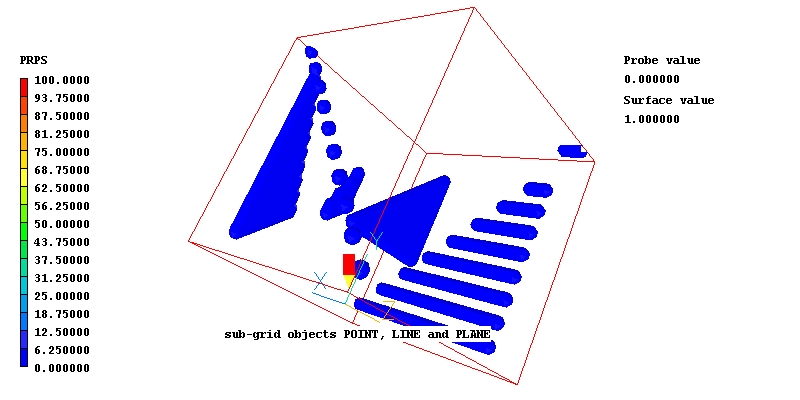
Points, lines and planes are all represented, the later by way of 'quadrilaterals' which have been reduced to triangles, as is always permissible, by having two cooincident vertices.
(d) Shapes made by restricting the PATCH size
The sphere object
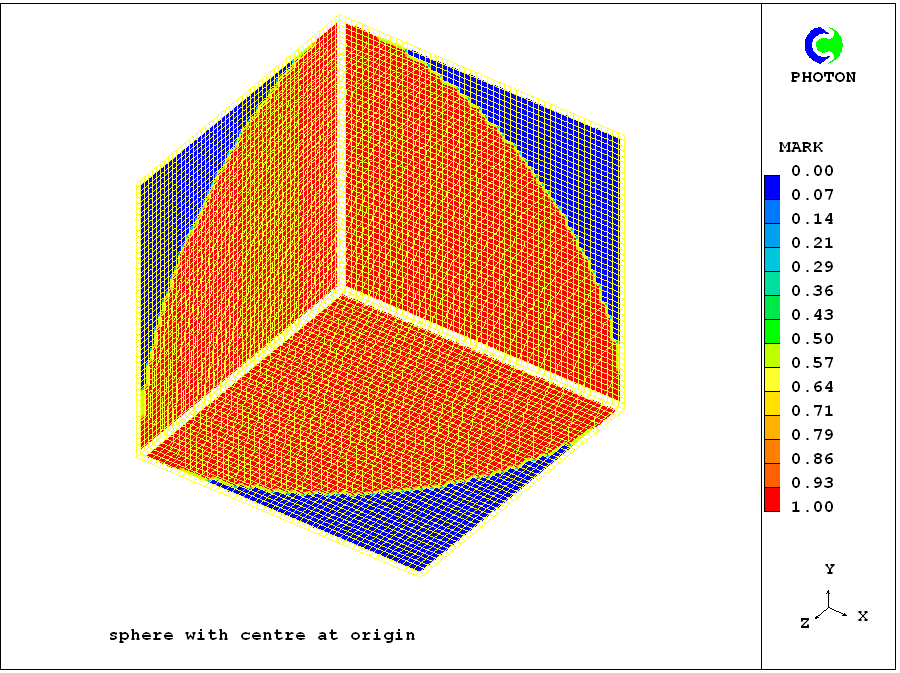
Core Input-File Library
case 386 concerns a sphere placed in a cartesian grid with its centre at the co-ordinate axis. Its radius, and the domain dimensions, XULAST, YVLAST and ZWLAST, are all equal to 1m.
When the patch referred to in the INFOB command is as large as the whole domain, the photon picture showing the contours and surface of the MARK variable are as shown here.
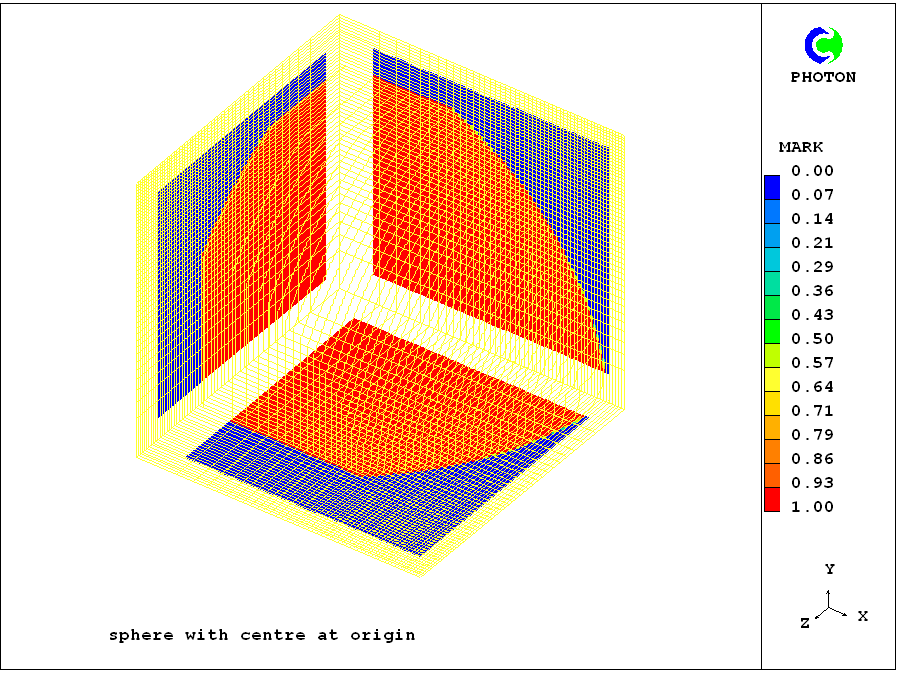
 When the size of the patch is reduced by 20% and 40% respectively in the y- and z-directions, the corresponding images are those shown below, that on the left corresonding to use of an indicial patch and that on the right to a
'dot-patch'.
They are of course identical.
When the size of the patch is reduced by 20% and 40% respectively in the y- and z-directions, the corresponding images are those shown below, that on the left corresonding to use of an indicial patch and that on the right to a
'dot-patch'.
They are of course identical.

 When however the distribution of the grid intervals is drastically changed by making the fourth arguments of the GRDPWR statements 0.5 rather than 1.0, the corresponding pictures are as shown below:
When however the distribution of the grid intervals is drastically changed by making the fourth arguments of the GRDPWR statements 0.5 rather than 1.0, the corresponding pictures are as shown below:
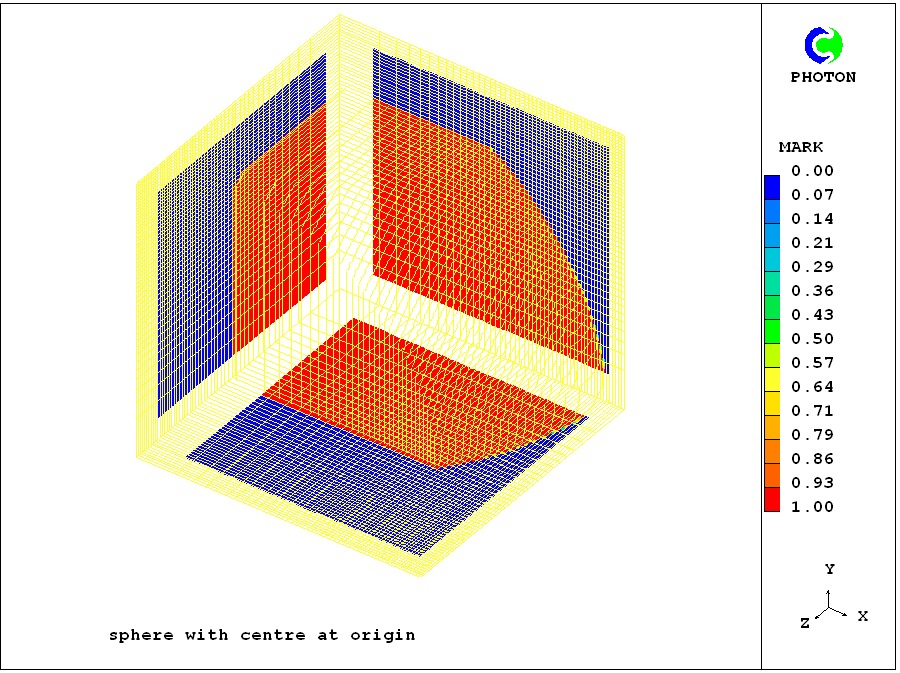
Evidently the shape of the object has changed for the indicially-sized patch; but it has remained constant for the geometrically-sized one. That the grid change is the same
in both cases is shown be the eqaual enlargement of the white bands used by PHOTON to high-light the co-ordinate axes.
Another example using spheres
Core Input-File Library
case 785 illustrates the use of a size-restricting patch to confine two concentric spheres to the layer of cells adjacent to a domain boundary, where they are used so as to represent two apertures, one disk-shaped and the other annular.
Of the two images below, that on the left displays the shape of the apertures by way of MARK contours, while that on the right shows the associated velocity vectors.
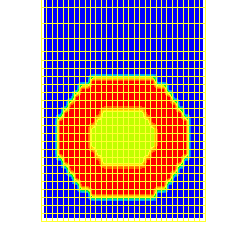
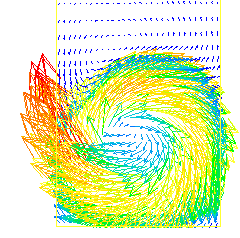
Of course, use of a finer grid would improve the circularity-appearance of the aperture edges. The use of a dot-patch makes this easy.
A final remark about the use of patches to limit object size
Although the just-demonstrated capability is sometimes useful, the fact that the surfaces of patches are by-definition aligned with the grid is a severe lmitation.
The use of 'subtraction', to be discussed in section (f) below, is much more powerful.
(e) Shapes made by using non-constant parameters
A pyramid made by use of the box function
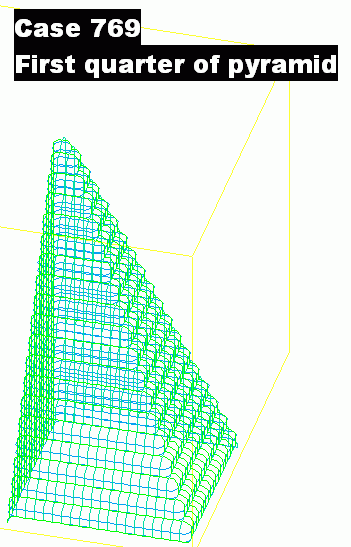
Core input-file library case769 shows how, by using expressions rather than constants as arguments, the BOX function can be used for creating the pyramid shown below.

Examination of the Q1 file shows that the pyramid is composed of four parts, of which the first, created by the lines:
(INFOB at PATCH1 is BOX(10,10,0,.5*(-ZG+20),.5*(-ZG+20),$
16*(-ZG+20.),0,0,0) with INFOB_1!poros)
while the second
is created by the lines:
(INFOB at PATCH1 is BOX(10,10,0,.5*(-ZG+20),.5*(-ZG+20),$
16*(-ZG+20.),0,0,.5*PI) with INFOB_1!poros)
in which the sole differences have been distinguished by the red font.
These first two quarters of the pyramid are shown below:

Let us now consider how it was that the quarter pyramids were created. The crucial steps were:
- The two red-printed 'rotation' arguments above, and the two further
ones which can be found for the third- and fourth-quarter statements,in
the case-769 Q1, namely 3*PI/2
and 1.5*PI, dictated that the four quarters were each rotated by an extra right
angle about the corner of the box at: x=10, y=10, z=0.
- Then the first and second 'size' arguments, namely:
5*(-ZG+20) and .5*(-ZG+20),
dictate that horizontal dimensions of the box
diminish linearly as the height zG increases. This gives the object its 'pointed'shape.
- The third 'size' argument, namely
16*(-ZG+20.)
proves to be much less
important; indeed the person who introduced it was probably not perfectly clear as to what he or she was doing; for to
insert ZG
produces
only porosity difference
at the very peak of the pyramid; then inserting ZWLAST
or
2.0*ZWLAST
or any large-enough number produces no further differences at all!
All that is important is that, when the EARTH solver module is deciding about each cell having co-ordinates xG, yG and zG whether it lies inside of outside the box, the box appropriate to that cell should have a z-dimension large enough to enclose it.
- Evidently, a truncated (i.e. flat-topped) pyramid could have been created by reducing the magnitude of the z-size argument.
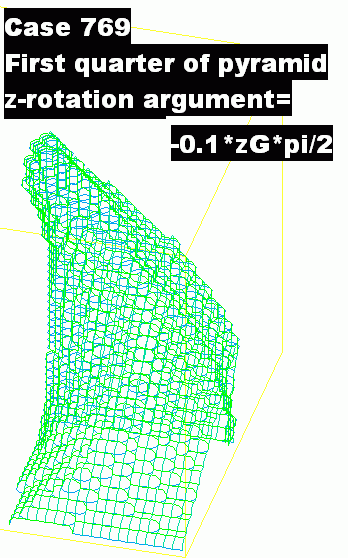
- Now that the secret has been revealed, it is obvious that there is no limit to the variety of shapes which can be created. Here for example is a shape created by making the z-rotation argument decrease as zG increases:
- Finally it should be mentioned that the four quarter-pyramids have all been given the same name, infob_1, in the case-769 q1. There is no objection to this; but, had it been desired to render display easier by giving each a diferent value of MARK, individual names would have been required.
Shapes made by use of the sphere function
Core input-file library
case749
shows how to create cones, spirals and a 'curved duct', by using the sphere object. It also enables tests to be made of the grid-independence of the In-Form-object settings.
Cartesian. cylindrical-polar and BFC grids are all represented.
The following hyperlinks lead to photon displays of the various shapes:
In the following table are shown the values of the arguments of the sphere function in the infob statement for the various cases. namely:
(infob at .patch1 is sphere(x0,y0,z0,rad) with infob_1)
| caseno | x0 | y0 | z0 | rad |
| 1 | xulast/2 | yvlast/2 | zwlast/2 |
xulast/4
|
| 2 | xulast/2 | yvlast/2 | zwlast/2 |
xulast/4
|
| 3 | xulast/2 | yvlast/2 | zwlast/2 |
yvlast/2
|
| 4 | xulast/2 | yvlast/2 | zg |
0.25*(:zwlast:-zg)
|
| 5 | xulast/2 | yvlast/2 | zg |
0.25*(:zwlast:-zg)
|
| 6 | yvlast | yvlast | zg |
0.5*(:zwlast:-zg)
|
| 7 | :xulast/2:*(1+0.8*cos(:PI2:*zg)) |
:yvlast/2:*(1+0.8*sin(:PI2:*zg)) | zg |
zwlast/10
|
| 8 | :xulast/2:*(1+0.8*cos(:PI2:*zg)) |
:yvlast/2:*(1+0.8*sin(:PI2:*zg)) | zg |
zwlast/10
|
| 9 | :yvlast:*(1+2*:rad:*cos(:PI2:*zg)) |
:yvlast:*(1+2*:rad:*sin(:PI2:*zg)) |
zg |
yvlast/4
|
| 10 | xg | :yvlast/2: | :zwlast/2:+0.25*sin(:pi2:*xg/xulast) |
yvlast/4
|
| 11 | xg | :yvlast/2: | :zwlast/2:+0.25*sin(:pi2:*xg/xulast) |
yvlast/4
|
The following points should be noted:
Library case 249 also possesses two boolean variables:
altercrt and alterbfc. Both were set false in all the cases shown so far; but, when set true,the former alters the cartesian grid and the latter alters the bfc one. They have been used for further testing the grid-independence of the In-Form object settings, with the results shown here.

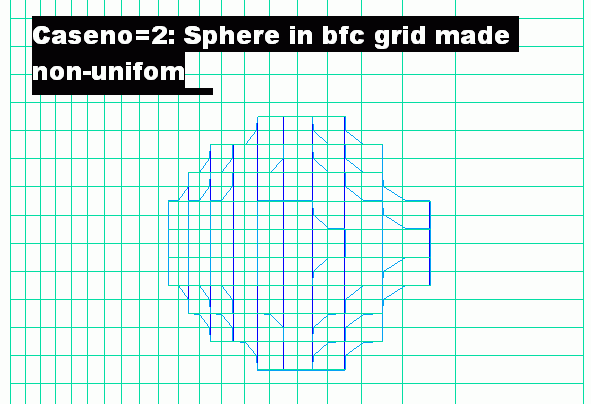
Clearly, although the distribution of the grid lines does affect the smoothness of its surface, the position of the sphere in cartesian space is not infuenced by it.
The bfc grid, it should be mentioned, was coarsened as well as distorted because the the execution of the
PIL do loop in
the Q1 file, by which the distortion was effected, is rather slow.
case 768 reveals that there is more than one way to create a spiral in a polar-coordinate grid; and its way of doiing so does create cross-sections which are more truly circular than those of case 749, as the next Photon image shows:
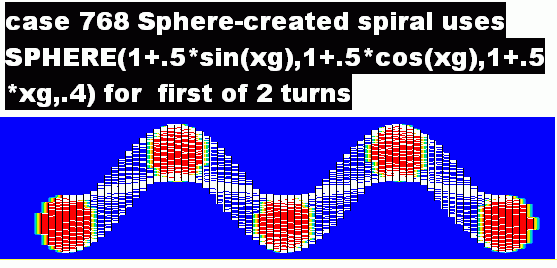
This method, as is seen, uses the angular coordinate xg
in the formula; therefore it is necessary to use two spheres for the two-turn spiral shown here. They can however, if desired, be specified in a single INFOB statement, as is explained by comments in the Q1 file of the case.
(f) Shapes made by adding and subtracting
- The two-turn spiral
- A disk at any angle
(g) 'Negative' objects
(h) Positions varying with time
(i) Shapes varying with time