H2 -> H + H
H2O -> H + OH
CO2 -> CO + O
H + H -> H2
H + O2 -> OH + O
O + H -> OH
Reactions releasing energy are called "exothermic"; those absorbing it are called "endothermic".
The amounts of energy involved are deducible from the thermodynamic properties of the reactants; and they are independent of the rates at which the reactions proceed.
Thermodynamics is a well-developed subject. Quantitative knowledge of energy releases exists for all reactions of interest to combustion specialists.
All chemical reactions are reversible, i.e. they can proceed in either direction. Thus:
H2 -> H + H and H + H -> H2
both proceed together.
"Equilibrium" is the state in which the rates of both "forward" and "backward" reactions are equal.
This occurs when [H2]/[H]2 has a specific value, called the "equilibrium constant", dependent on temperature. Here [H2] stands for kg.moles of H2 per m3; etc...
Typically, the reaction
R1 + R2 -> R3 + R4
proceeds at a rate given by the "Arrhenius" expression:
![]()
where const1, const2, const3 and const4 are specific to the reactants in question, and T is the absolute temperature.
Although incomplete, in that many chemical reactions remain to be fully explored, chemical kinetics has collected much more information than it is practicable to incorporate into engineering-scale combustion simulations.
For example, it is known that the burning of a hydrocarbon in air proceeds by way of hundreds of distinguishable chemical reactions, involving tens of intermediate chemical species. Only the initial and final states are represented by:
1 kg of fuel + s kg of oxygen -> (1+s) kg of products.
where s is the stoichiometric ratio, which guarantees complete combustion.
The SCRS postulates that combustion does proceed via
fuel + oxygen -> products
WITHOUT intermediates.
This reaction is taken as irreversible; i.e. the rate of the reverse reaction is presumed to be very low.
The energy released, called the "heat of combustion", is taken as independent of temperature; this implies equality (even constancy) of specific heats of reactants & products.
The enthalpy of a mixture of fuel, oxidant and products can be taken as given by:
![]()
where:
Cp is constant-pressure specific heat,
T is absolute temperature,
H is heat of combustion and
mfu is mass fraction of unburned fuel.
The ratios of the masses of fuel, oxidant and products engaging in a reaction are: 1, s and (1+s) respectively, where s is a constant.
Typically, s = 3.5, when the fuel is a hydrocarbon and the oxidant is undiluted oxygen.
An often-used extension of the SCRS definition is that the diffusion coefficients of fuel, oxidant and product are all equal to each other, and to the diffusivity of heat; so their Prandtl/Schmidt numbers are equal.
This is not far from the truth for laminar gaseous flow; and it is very close to the truth for turbulent fluids.
If this assumption is made, then it can be proved (Reference 1) that the following quantities are 'conserved properties of the fluid' in the sense that source term in the differential equations which govern their distribution are zero:
It is easy to see that (fu - ox/s) is always conserved when diffusion is not present; for chemical reaction causes both fu and ox to diminish in proportion, the constant of proportionality being s.
Equality of diffusion coefficients entails that, when the differential equation for ox is divided by s and subtracted from the equation for fu, not only does the source term vanish but also the dependent variables appear only in the form of their difference fu - ox/s.
A similar argument prevails for fu + pr, which moreover can then be recognized as representing the mass fraction of material derived from the fuel-bearing inflow stream.
This quantity is of such importance that it is often used as a dependent (i.e. solved-for) variable in combustion calculations, often being called the 'mixture fraction' with the reserved name 'MIXF'. See for example core-library case 492.
If fu + pr/(1+s) is given the symbol mf, it is easy to
deduce the mass fraction of product as being given by:
pr = ( mf - fu ) * (1+s)
Similarly, the oxidant mass fraction ox can be deduced from
fu and mf from the equation:
ox = (1-f) + s * ( fu - mf)
An important consequence is that it is possible to describe the composition of a reacting mixture by just two variables, for example:
mfu = the mass fraction of unburned fuel, and
f = the "mixture fraction", i.e. the mass of material originating from fuel, per unit mass of mixture, regardless of whether it is burned or not.
At the stoichiometric ratio, s, the mixture fraction is:
f = fstoic = 1 /(1 + s)
In the SCRS, the products are represented by a single mass fraction, which will usually represent a mixture of several chemical species.
The relationships between the mixture fraction, f, the mass fraction of oxidant and mass fraction of products can be shown to be as follows:
f < fstoich ; mfu = 0 (all fuel burnt)
![]() (surplus oxidant)
(surplus oxidant)
f > fstoich ; ![]() (surplus burnt)
(surplus burnt)
mox = 0 (all oxidant consumed)
Any f ; ![]()
mprod = 1 - mox - mfu - mdil
where mox0 and mdil0 are oxygen and diluent mass fractions at the inlet.
These relationships can be shown graphically as:
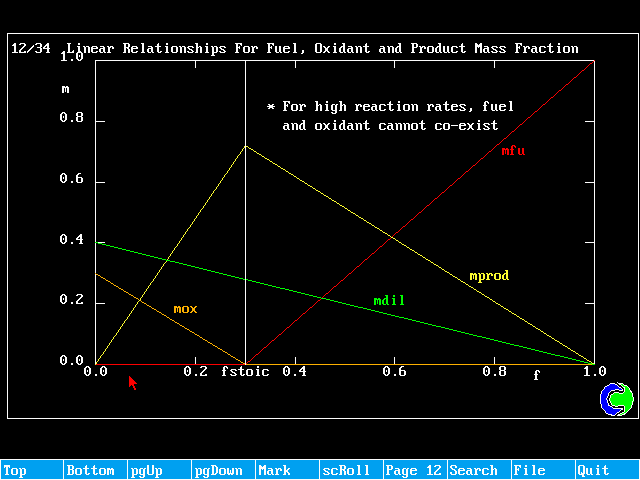
Linear Relationships For Fuel, Oxidant and Product Mass Fraction
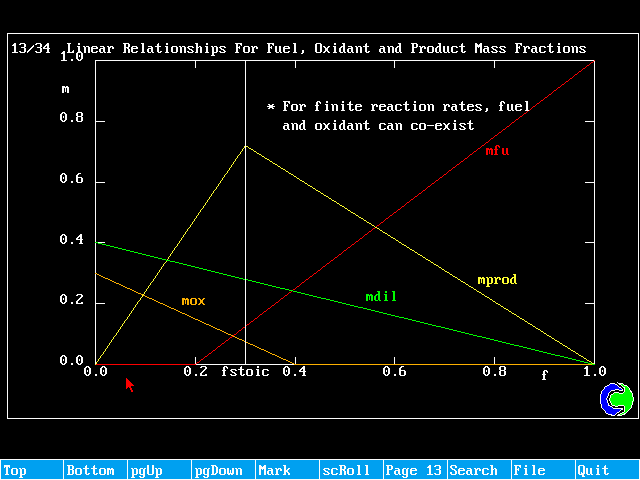
Linear Relationships For Fuel, Oxidant and Product Mass Fractions
The f equation has no source term.
The h equation can has a source term resulting from absorption and emission of radiation; but this is often small enough to be neglected.
If so, temperature can be deduced from h via:
![]()
where the mixture specific heat is calculated from the individual species specific heats.
The mass fraction of oxidant, mox, can be deduced from
![]()
The mfu equation has a reaction-rate source of the form:
source of fuel = - const ![]() mfu x mox x function of T
mfu x mox x function of T
When the reaction-rate constant is large, there is no need to solve for mfu; it depends only on f, and can be deduced from:
![]()
This is the 'mixed-is burned' assumption.
The mass fraction of products can be deduced from:
mprod = 1 - mox - mfu
Density can be calculated from the Ideal Gas Law as:
![]()
where the mixture molecular weight, W, is calculated from the individual species molecular weights.
< rate(rctd) > does NOT equal rate(<rctd>)
because of the non-linearity of rate; and
< mfu * mox > does NOT equal < mfu > * < mox >
because mfu and mox may be finite only at different times.
Since CFD codes compute only < rctd >, < mfu > and < mox > but need < rate > , new formulae are needed for turbulent flow.
No certain or universal method has yet been discovered; but some guesses have proved lucky.
Experiment shows that reaction rates are often more greatly affected by local turbulence than by chemical-kinetic factors.
The eddy-break-up model (Reference 2) rests on the hypothesis that ONLY turbulence and fuel concentration affect the rate.
The first version was:
The second version was:
Both work fairly well; but they are only approximate.
The f and mfu equations are created from two of the spare concentration equations. The mox and mprod mass fractions are deduced as above, and are then stored, for printing and plotting.
For the rate-controlled model, various expressions for the reaction rate are coded into the subroutine GXCHSO. They are activated by appropriate PATCH and COVAL commands for the mfu equation.
The calculation of density from the Ideal Gas Law, but with a mixture specific heat, is coded into GXRHO, whilst the deduction of temperature from the SCRS definition of enthalpy can be found in GXTEMP. mox and mprod are also deduced in GXTEMP.
The SCRS can be activated in the VR-Editor from the Models panel of the Main menu. The diffusion-controlled model is obtained by selecting '3-Gases mixing', and the rate-controlled model by selecting '3 Gases kinetic'. The Settings dialog for the combustion models allows all the relevant parameters to be set.
The following PIL settings are common to both the diffusion-controlled and rate-controlled models:
NAME(16)=MIXF; SOLVE(MIXF) - the f equation
STORE(OXID, PROD) - storage for mox, mprod
TMP2A = fstoic (= 1 / (1 + s))
TMP2B = the heat of reaction, H
CP1 = GRND10
CP1A = the specific heat of the fuel
CP1B = the specific heat of the product
CP1C = the specific heat of the oxidant
RHO1 = GRND6 - activate Ideal Gas Law with mixture molecular weight
RHO1A = the molecular weight of the fuel
RHO1B = the molecular weight of the oxidant
RHO1C = the molecular weight of the product
CHSOA also has to be set to fstoic for the eddy break-up model.
The diffusion-controlled model then requires:
STORE(FUEL) - storage for mfu.
TMP1 = GRND7 - deduction of temperature from T = (h - mfu x H) / cp with deduction of mfu from f.
The rate-controlled model requires:
SOLVE(FUEL) - solve the mfu equation
TMP1 = GRND8 - deduction of temperature from T = (h - mfu x H) / cp
A reaction-rate source must also be activated.
For laminar flows, several reaction rate sources have been provided. These are listed below.
Power-law temperature-dependent reaction-rate. The resulting source per unit volume is:
![]()
This is activated by:
PATCH (CHSO, VOLUME, IF,IL, JF,JL, KF,KL, TF,TL) COVAL (CHSO, FUEL, GRND5, 0)
The reaction rate constants, a and b, are passed via:
CHSOA = 1 CHSOB = -1 / fstoic [ = -(1+s) ] CHSOC = 1 / fstoic - 1 [ = s ] CHSOD = b CHSOE = a
![]()
This is activated by:
PATCH (CHSO, VOLUME, IF,IL, JF,JL, KF,KL, TF,TL) COVAL (CHSO, FUEL, GRND6, 0)
The reaction rate constants, a, E and R, are passed via:
CHSOE = Reference temperature (0 if T is in K) CHSOD = E/R CHSOA = a CHSOB = -a / fstoic [ = -a x (1+s) ] CHSOC = a * (1 / fstoic - 1) [ = a x s ]
Power-law fuel-mass-fraction-dependent reaction-rate. The resulting source per unit volume is:
![]()
This is activated by:
PATCH (CHSO, VOLUME, IF,IL, JF,JL, KF,KL, TF,TL) COVAL (CHSO, FUEL, GRND7, 0)
The reaction rate constants, a and b, are passed via:
CHSOA = a CHSOB = b
For turbulent flows, the second form (see section 2.6 above) of the eddy-breakup reaction-rate is provided. The resulting source per unit phase mass is:
![]()
This is activated by:
PATCH (CHSO, PHASEM, IF,IL, JF,JL, KF,KL, TF,TL) COVAL (CHSO, FUEL, GRND9, GRND9)
The reaction rate constant, a and the stoichiometric ratio,s, are passed via
CHSOB = a CHSOA = 1 / (1 +s) [= fstoic]
The rate controlling parameter CHSOB is commonly set to unity.
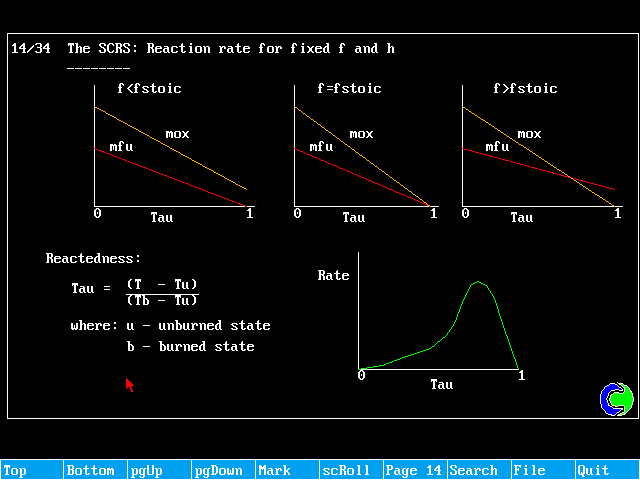
If the fuel and oxidant are fully pre-mixed, and the distribution of f is uniform, it becomes possible to solve just one equation, termed the "reactedness".
The reactedness can be regarded, for adiabltic situations as a non-dimensionalised temperature. If u denotes the unburnt state, and b the fully burnt state, the reactedness can be then be defined as:
![]()
Tu and Tb will be known experimentally.
Solution of the reactedness equation is activated by:
NAME(H1) = RCTD - Change name of H1 to RCTD
SOLVE (RCTD) - Solve it.
TERMS (RCTD, N, P, P, P, P, P) - Remove the built-in sources.
The temperature can be recovered by:
TMP1 = GRND2 - Selects T = a + b x H1
TMP1A = Tu
TMP1B = Tb - Tu
If pressure changes are small, density can be calculated from the Ideal Gas Law at constant pressure. This is activated by:
RHO1 = GRND2 - Selects rho = 1 / (a + b x H1)
RHO1A = R x Tu / Pref [ = 1 / rhoref ]
RHO1B = R x (Tb - Tu) / Pref [ = 1 / delrho ]
If the pressure changes are not negligible, then the full Ideal Gas Law can
be used:
RHO1 = GRND5 - Selects rho = b * (P1+Pref) / T
RHO1A = 0.0
RHO1B = 1/R
RHO1C = 1/gamma
PRESS0 = Pref
The reactedness equation needs a reaction-rate source. As only one equation is being solved, only the built-in fuel-mass-fraction-dependent source can be used, as all the others have a mfu x mox multiplier. This source is coded as:
![]()
The PATCH setting will be:
PATCH (CHSO, VOLUME, IF,IL, JF,JL, KF,KL, TF,TL) COVAL (CHSO, RCTD, GRND7, 1.0) CHSOA = a CHSOB = b
The setting of VALue to 1.0 ensures that the source falls to zero as rctd approaches unity, as expected from the reaction-rate vs reactedness diagram.
The values of the reaction constants, a and b, can be based on experimental data, and numerically 'tuned' to give the expected laminar flame speed.
As supplied, the SCRS is applicable to single fuel, single oxidant systems, e.g.
hydrocarbon + air -> products
The fuel and oxidant streams can be separate, or pre-mixed. Secondary oxidant (or fuel) inlets are allowed.
The flow can be laminar or turbulent, steady or transient, and any coordinate system can be used.
The diffusion-controlled "mixed-is-burnt" model is applicable only to cases where there are separate inflows of fuel and oxidant. It cannot be used for pre-mixed cases. It also assumes infinite (very high) rates of reaction.
In laminar flows, the reaction rate is normally temperature dependent. The rate parameters can be found from experimental data.
For turbulent flows, the situation is far less clear. The eddy-breakup model works well for some cases, but not always. The two-fluid model may offer further insight into turbulent combustion behaviour.
If fuel and oxidant are uniformly pre-mixed, the reactedness model offers a simple way of studying laminar flame spread at low computational overhead.