Examples are:-
Definition of a phase
The above examples employ the word "phase" in the sense customary in
thermodynamics, where the liquid, solid and gas phases are
distinguished.
However, a broader definition of phase is used in PHOENICS. This allows sand particles of different densities, or steam bubbles of different sizes, or gas eddies of different temperatures, also to be regarded as different phases.
Often, the multiple phases in the complete domain become sharply separated. This happens, for example, when the gas flame beneath a domestic kettle is switched off; for the bubbles rise, the suspended droplets fall, and a plane unbroken surface forms between the steam and the water.
The flow is then often called a fully-separated or free-surface flow.
Both intermingled and separated flows are considered in this encyclopaedia article.
When many phases are present, it is impractical to solve full sets of Navier-Stokes equations for all of them.
In this method, therefore, only one set of differential equations is solved, to give the mixture-mean velocities at each point and time.
Then separate sets of equations are solved, one for each phase, which govern its relative velocities, i.e.their differences from the mean.
The latter equations are algebraic ones, which are derived from the Navier-Stokes equations by neglect of second-order terms.
This entails that the relative velocities are computed by reference only to the local pressure gradients, the body forces and the inter- phase friction.
The volume fractions occupied by each phase, at each point and time, are calculated at the same time.
This method is referred to in the PHOENICS documentation as the "algebraic-slip" method, with the abbreviation ASLP. Elsewhere in the scientific literature, it is sometimes called the "drift-flux" method.
It is embodied in the Advanced Multi-Phase Flow option of PHOENICS; and it makes use of the open-source Fortran file GXASLP.FOR .
Click here for a lecture on the algebraic-slip method
This method is especially useful for simulating sedimentation and other processes, for example the separation of oil, gas and water in a centrifuge.
An example of this kind now follows.

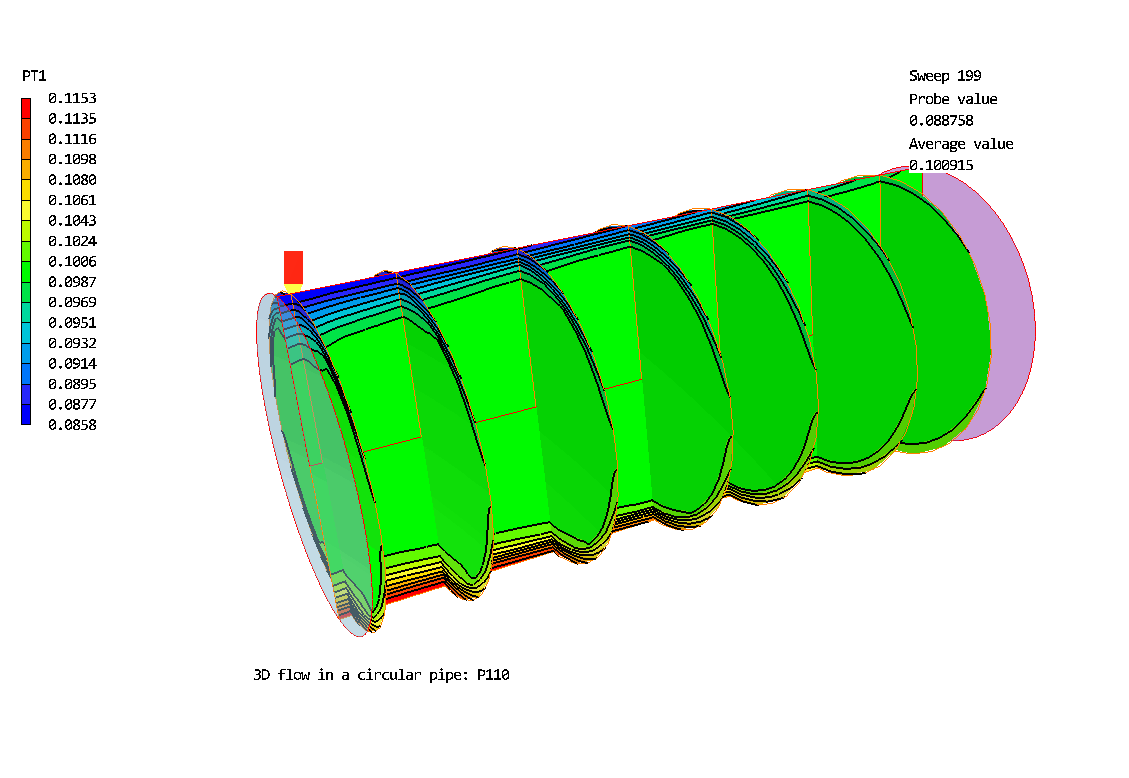
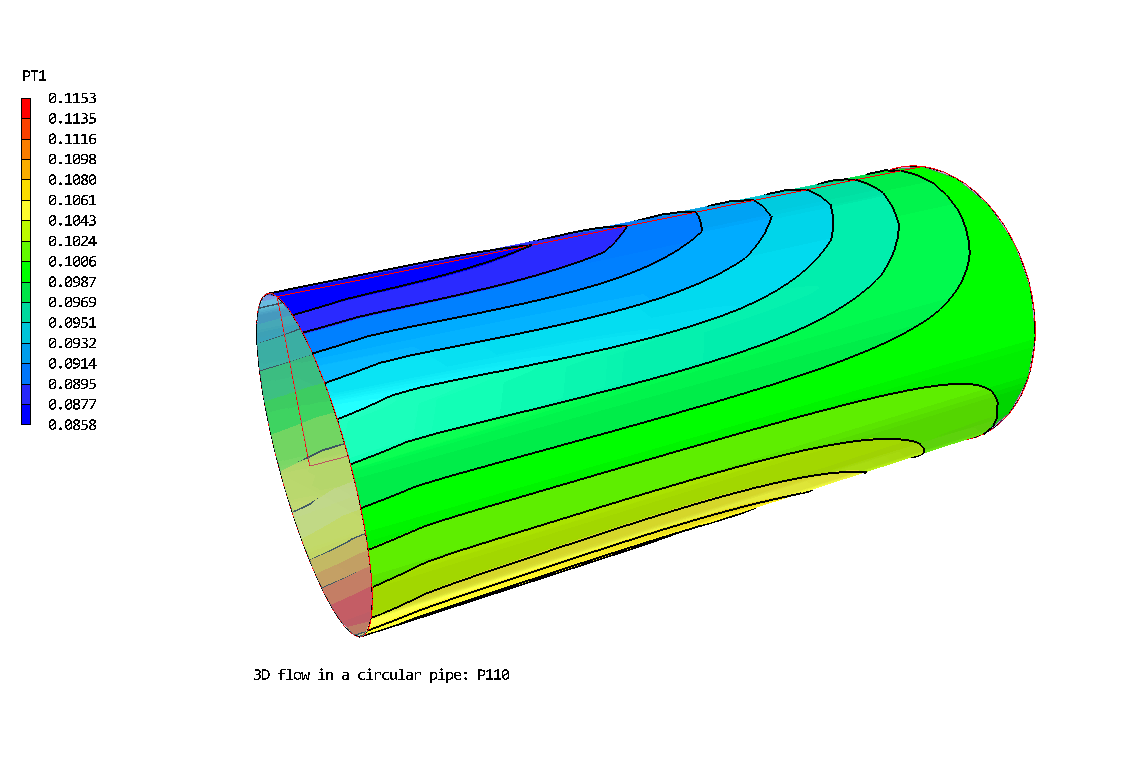
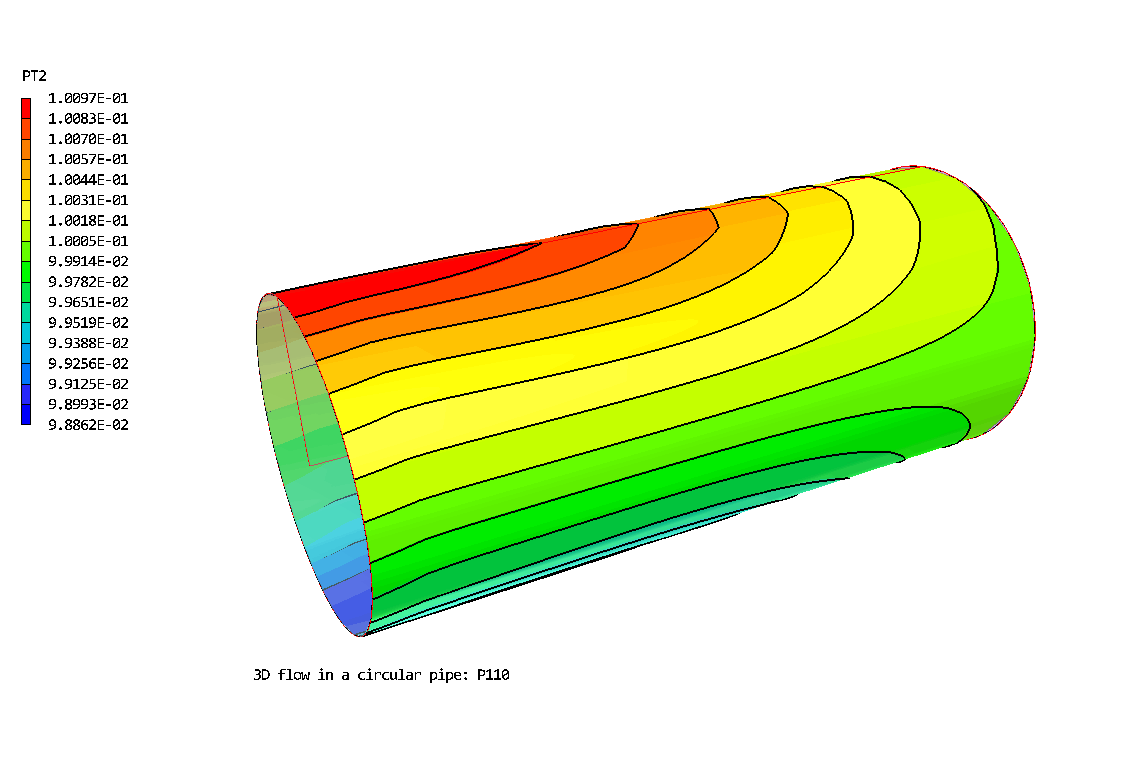
The 3D Polar grid: 20 * 20 *30. Flow is from left to right. The geometry has been expanded by a factor of 5 in the radial direction.

Contours of pressure
Contours of the larger-diameter (particle air concentration
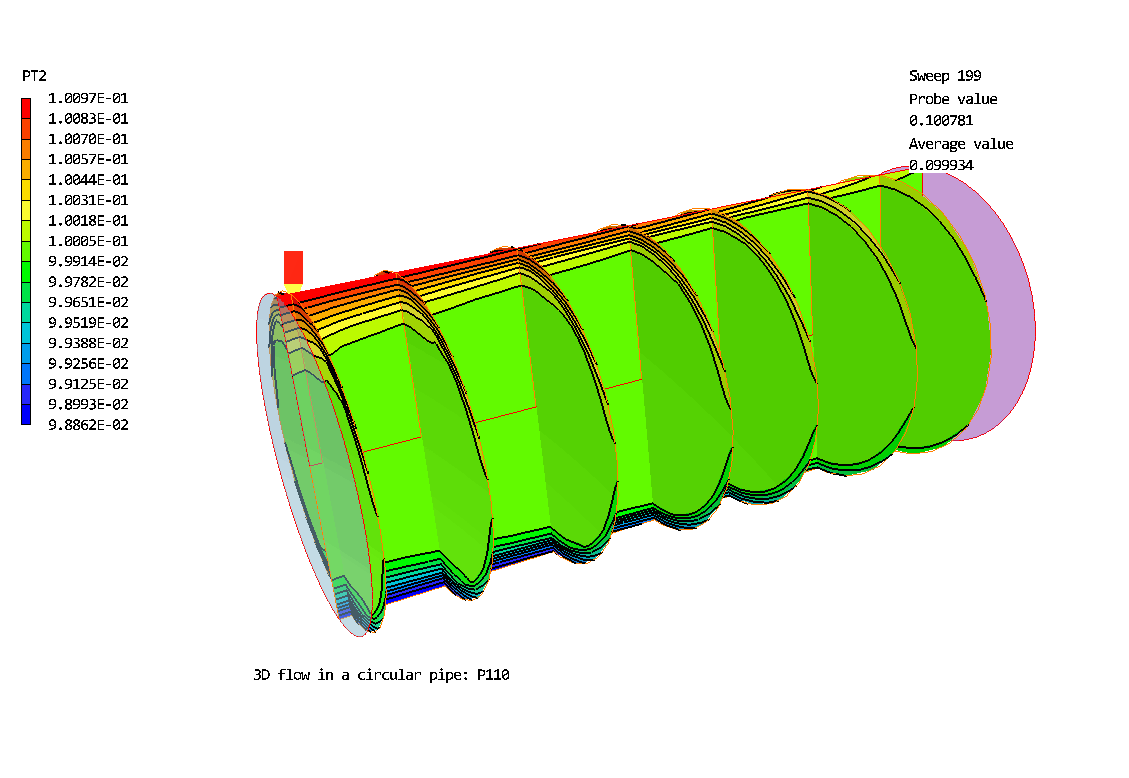
Contours of the smaller-diameter particle air concentration
See also the following Applications Album entry
Method (3) treats the two (or more) fluids as a single fluid subject to discontinuities of density, viscosity and composition.
These discontinuities, i.e.the inter-fluid surfaces, are tracked as they move through the domain of interest, by solution of the individual continuity equations of each fluid.
Three tracking procedures are available, namely:
click here for a comparison of these methods.
Heavy drop falling through light drop
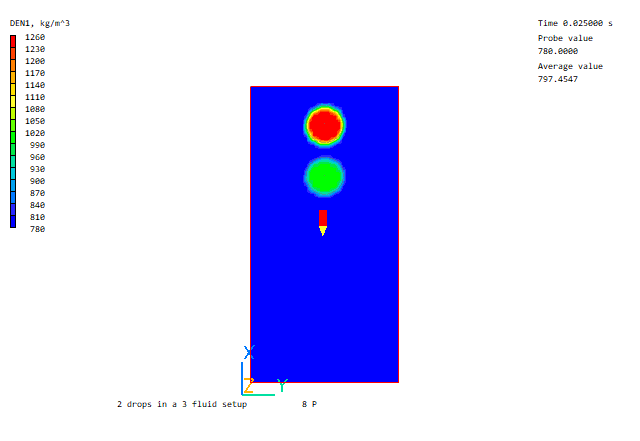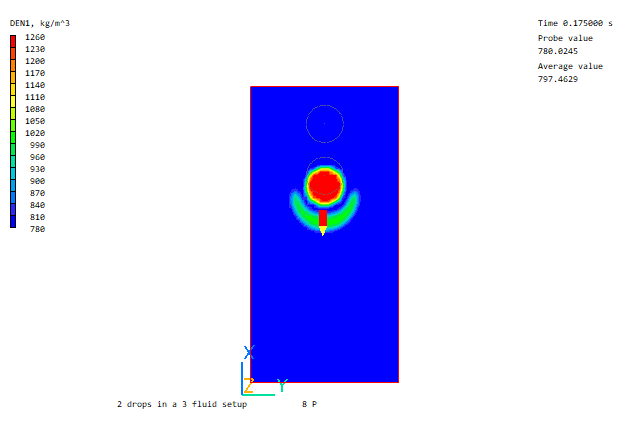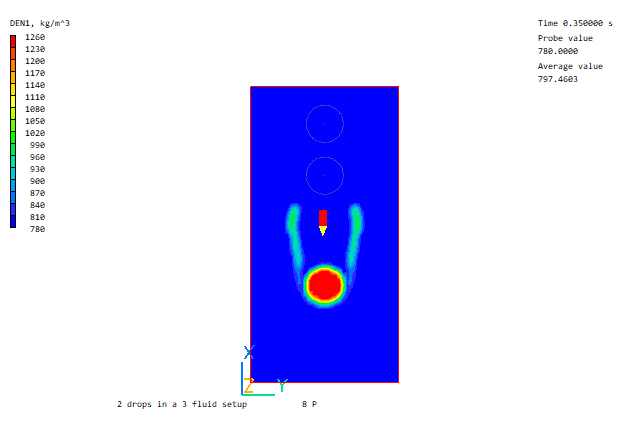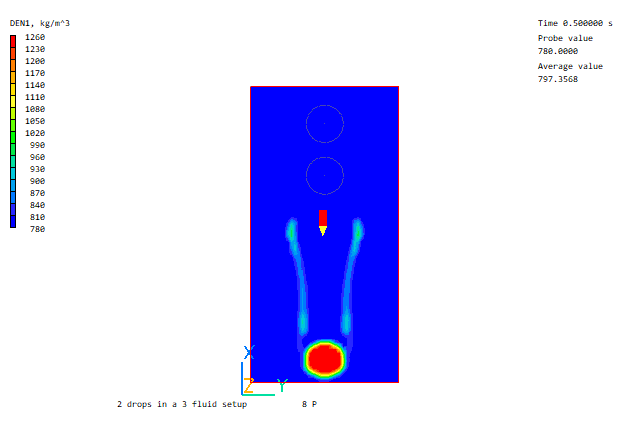
Further Volume of Fluid examples
Method (4) is embodied in the GENTRA (i.e.GENeral TRAcking) option of PHOENICS.
The particles (or groups of particles) are tracked by solving the Lagrangian equations of motion, with full interactivity between the particulate and the continuous phases.
Heat, mass and momentum transfer can take place between the particulate and continuous phases; and the particles can undergo phase change and chemical reaction. They may also radiate.
Allowance is made for the particles to stick to walls which they hit, to slide along them subject to friction, or to bounce off with various coefficients of restitution.
GENTRA has found many applications in chemical engineering, power engineering and aeronautics, e.g.the icing of aircraft-engine intakes.
Examples of the application of the above methods to industrial and scientific flow simulations will be found in the Application Album.
For further information, see the PHOENICS Encyclopaedia entries: IPSA, ASLP, VOF, SEM, HOL, GENTRA, and also the Lectures on PHOENICS at the top level of POLIS.
See also the Encyclopaedia article on Multi-Fluid Models of Turbulence, and the lectures accessible from the top POLIS menu.
 Body-fitted grid
for a spray
dryer
Body-fitted grid
for a spray
dryer
 Gas flow field
Gas flow field
 Particle trajectories
Particle trajectories
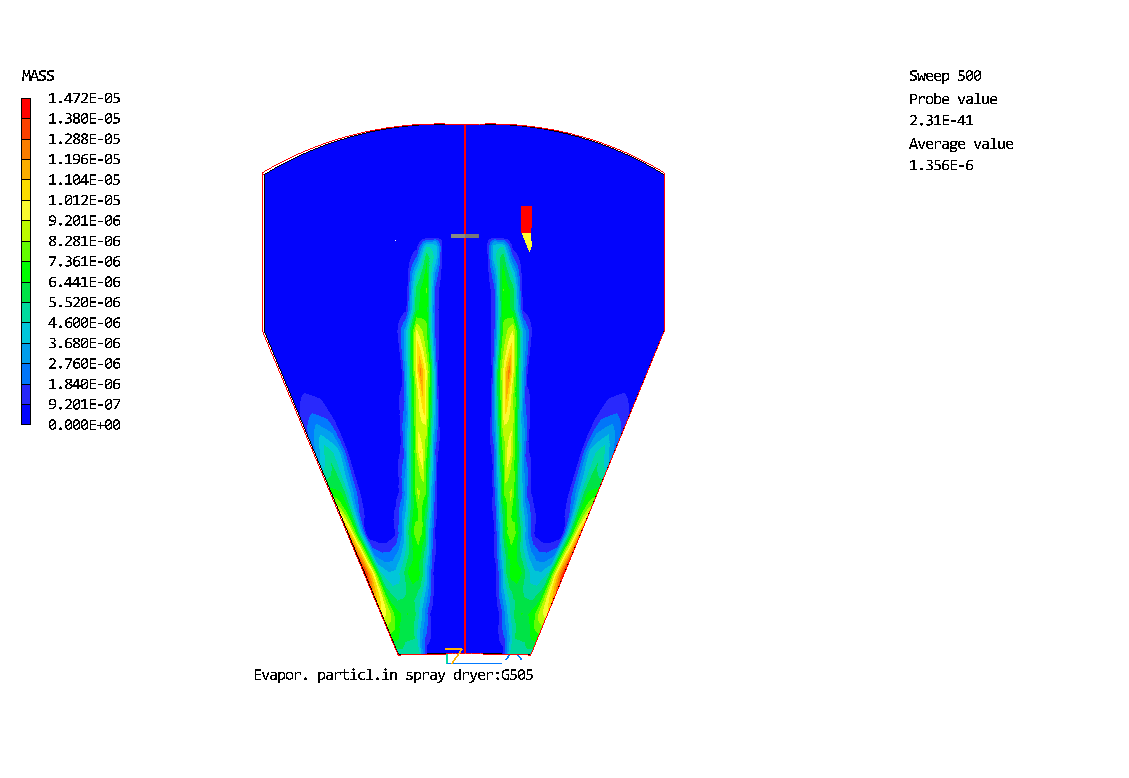 Contours of vaporisation rate
Contours of vaporisation rate
 Contours of vapor mass fraction
Contours of vapor mass fraction